5 Feedback control theory

• analyzing existing controlers, in the frequency domain
• noise is all frequencies
• unstable pole-zero cancellation

Stability of feedback systems

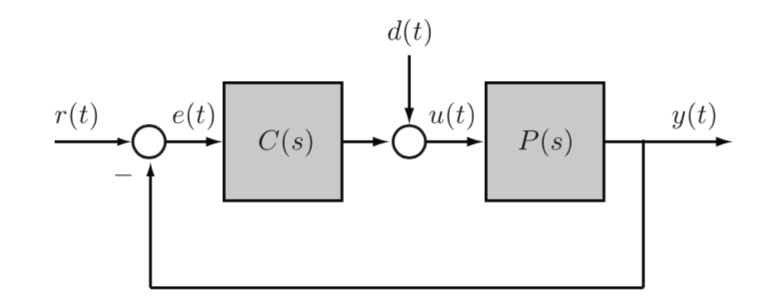
• system has 6 transfer funcitons from \((r,d) \times (e, u, y)\)

Definition: The feedback system is input-output stable if e,u, y are bounding signals whenever exogenous inputs are bounded (all transfer functions are BIBO stable)

• notice in ex 5.2.5 since there are poles, D to E is not stable, so not I/O stable
• when connecting our plant to the controller, P can cancel poles to achieve stability

We could try to find every possible transfer function in a system, but we want a way to test stability without

Definition: the characteristic polynomial of the feedback system is \(\pi(s) := N_p N_c + D_p D_c\) is the denominator of the four transfer functions from (r,d) to (e,u)

• if we want to check IO stability, we just need to look at this polynomial!