Combinatorics

Summary

• fibbonacci numbers come from the number of compositions from the set {1,2}
• the set of binary strings can be represented through a cartesian power: {0,1}ⁿ
• binomial theorem is intuitively, the number of ways to get each final term, written as combinations of (1+x) terms, choosing either 1 or x
  • binary strings produce similar results, when applying a generating series
• two conjectures that lead to pascal's triangle are: 1. nCk = nC(n-k) and 2. nCk = (n-1)C(k-1) + (n-1)Ck
• generating series for a finite set use a weight function w to map each element to a natural number
  • model a lot of counting problems using generating series; simply find a weight function and count the number elements of a given weight
  • they act as a simple numerical function that represents a physical counting problem, where Φ(1) = |S|, and Φ'(1) is the sum of the weights of all elements (since the power represents the weight and coefficient is the count)
• a formal power series is ^∞∑_i=0 a_ixⁱ, of only rational coefficients (note that lots of functions are considered FPS, with lot's of 0 coefficients, so it's not necessarily infinite)
  • like a power series (think taylor series) but differs in that we allow n to be infinity, and don't consider that x is a number thus ignoring the idea of convergence
• k partitions of S are A1, A2... Ak s.t S = A1 u A2 ... u Ak and Ai n Aj = ø
• Sum Lemma allows us to partition generating series
• Product Lemma allows us to combine and break down generating series with cartesian products
• if sets A,B of binary strings, then AB is unambiguous iff there is a bijection between AB and A x B

Introduction

Study of finite or countable discrete structures

• discrete mathematics involves structures and processes that can often be enumerated by integers
• includes counting the structures of a given kind/size
• deciding when certain criteria is met
• four colour theorem: any separation of plane into contiguous regions can bel coloured with no more than four colours so that no two adjacent regions have the same colour
• Fibbonacci from permutations of {S,L}, where S is length 1, L length 2, n = total length
  • compute # of permutations of a set of length n, happens to equal the nth Fibbonacci #

A composition of a non negative integer n is a sequence where m1,..mr are positive integers and n = ∑m1...mr

• Fibbonacci is the number of compositions of an integer, where the elements are 1 or 2
• in example, SSSS -> (1,1,1,1), and SLS -> (1,2,1)

Binary Strings have some length n, and are a sequence of 0s and 1s, with 2ⁿ possibilities

• Cartesian product of sets A and B are all ordered pairs of their elements; |A x B| = |A| • |B|
• Cartesian power Aⁿ is the set of ordered n-tuples of elements from A; |Aⁿ| = |A|ⁿ
• set of binary strings with length n can be expressed as the cartesian power: {0,1}³ = {000,001...111}

Binomial Coefficients help us tackle "enumeration problems", like how many k-element subsets are there of an n-element set, which we recognize to be the nCk (combinations)

• [n] = {1,2,...n}, then a permutation of [n] is a rearrangement of its elements, with n! total permutations written as k-tuples
• combinations are different ways to choose k things from n things
• Pascal's triangle shows the number of combinations for a given column and row

Combinatorial Proof is any proof involving some kind of counting argument

• example is the binomial theorem

Binomial Theorem: (1+x)ⁿ = ∑ (nCk)x^k

• intuition: we have n (1+x) terms. When multiplying these terms, we either choose the 1 or the x
  • when multiplying we end with n+1 terms x⁰ + ... + xⁿ
  • to get the coefficients of these terms, we want to look at how many combinations we get for choosing x:
  • we get nC0 x⁰ + ... + nCn•xⁿ
  • we are counting the number of ways each x^k term occurs during multiplicative expansion
• we call each (nCk) a binomial coefficient
• Proving conjecture 1: nCk = nC(n-k) algebraically is simple
  • but we need to do combinatorial proofs, and get a more intuitive sense for the statement
  • intuitively, it is suggesting that we're counting the complement

Show nCk = nC(n-k) with a combinatorial proof

• look at both sides, and what they're counting, then understand why they're are equal and formailze
• let S be the set of k-subsets of [n]
• let T be the set of (n-k)-subsets of [n]
• to formailize counting, we will form a bijection from S to T
• forall members A in S, f(A) [n]\A; set subtraction, so notice f is mapping an element to its complement
• f^-1: T -> S
• f^-1(B) = [n]\B forall B in T
• since we have a bijection between S and T, then |S| = |T|

Show the second conjecture is true

• S is the set of all k-subsets of [n]
• idea: partition S into two disjoint sets S1 and S2
• S1 is the set of all k-subsets of [n] that contain n
• S2 is the set of all k-subsets of [n] that do NOT contain n
• we can see they are disjoint, and so |S| = |S1| + |S2|
• then we can see |S1| = (n-1)C(k-1)

Prove (n+k)Cn = k∑i=0 (n+i-1)C(n-1)

• intuitively, say we have 5C3, if we partition based on the last number (5), then we have 4C2 possible subsets, also with 4 fixed, we have 3C2 possible subsets, and fixing 3, we have 2C2 subsets

Proof:

• Let S be the family (means set) of n-subsets of [n+k] |S| = (n+k)Cn
• forall sets A in S, the largest element of A is in {n,n+1,...,n+k}
• partition S into smaller families based on the largest element
• Let S_i be the family of n-subsets of [n+k] whose largest element is n+i where i in {0,1,...,k}
  • notice, Si n Sj = ø forall distinct i,j
  • also S = So u S1 u S2 u ... u Sk

Generating Series

Helps us with a very general enumeration problem

Let S be a set of objects, N = {0,1,2...}

• a weight function of S is a function w:S -> N which assigns to each σ in S a non-negative integer w(σ) called the weight of σ
• Example: S = binary strings of length 4. For σ in S, weight of σ, w(σ), is the number of 1s in σ
• this gives us a General Problem: How many elements of S are there of weight k?

So the generating series for S with respect to the weight functon w is:
Φ_S(x) = ∑(σ in S)x^w(σ)

• brute forcing binary strings of length four, and applying the weight function
  • Φ_S(x) = x⁰ + 4x⁰ + 6x¹ + 4x² + x³
  • Φ_S(x) = (1+x)^4
• observe that the coefficient of x^k is the # of elements of weight k in S

Theorem 1.6.3
Let Φ_S(x) be the generating series for a finite set and weight function w. Then

1. Φ_S(1) = |S| (follows intuitively by the fact that at 1, it is defined to be the sum of all coefficients)
2. Φ_S'(1) = sum of all weights
3. Φ_S'(x)/Φ_S(x) = average weight of an element in S

Example:

S is the set of all binary strings. Then we have 2^k possible strings

• now se have

Formal Power Series

• FPS is a power series of the form A(x) = infinity ∑0 a_nxⁿ = a₀x⁰ + a₂x² + ...
• we can encode all these numbers as (1+x)^n, not really as a function but think of it as encoding/short form

Let A(x) and B(x) be two FPS

• it is natural that equality of two power series implies equal coefficients
• operation: additions, add the coefficients for each term
• we can multiply by a constant, where each coefficient is multiplied by the coefficient
• multiply two FPS, just think back to foil/binomial expansion; there's no fancy/fast form
  • thinking about the table of coefficients, this form looks like: (infinity)∑n=0( n∑j=0 a_jb_n-j)xⁿ
• division, if A(x)B(x)=1, then B is the inverse of A. But the inverse may or may not exist, but when it does exist, it is unique
  • let's look at what it means for FPS to have an inverse
  • we want A(x)B(x) = 1 = 1x⁰ + 0x¹ + ...
  • a0b0 = 1, and since a0 is given, it must not be 0 and b0 = 1/a0. Now that we know what b0, we can then solve for b1 for the x¹ term

Examples applying operations:

• does x+x^2 have an inverse? No, since the coefficient of x^0 = 0
• does 1-x have an inverse? Yes; (1-x)^-1 = 1 + x + x² + x³ + ... notice this is a geometric series, but we want to avoid the concept of limits, don't think of them as functions, but rather an encoding of numbers for the purpose of counting combinatorial objects

Substitution (composition)

• Let A(x) = inf-sum a_nx^n and B(x) = inf-sum a_n•x^n (both FPS)
• substitution/composition is A(B(x))
• substitution should result in another FPS, so when is it allowed/when is A(B(x)) a FPS?
  • well, when B(x) has a constant or coefficient for x⁰, then the result is not an FPS because the constant will result as infinity (constant is not finite)
• formally, if A(x) and B(x) are FPS, if the constant term of B(x) = 0, then the substitution of B(x) into A(x) is also a FPS

More Generating Series Tools

• Sum Lemma (1.8.1): let S be a set with weight function w, and let (A,B) be a partiton of S. (S = A u B and A n B = ø). Then &Fi;_S(x) = &Fi;_A(x) + &Fi;_B(x)
  • is intuitive, written at ∑ + ∑
  • if the intersection of A and B is not empty, add a subtraction term - &Fi;_{A n B}(x)
  • it follows that we can take the summation of weight functions applied to any amount of partitions
• suppose we want to find the number of ways to make $n for l loonies and t toonies. Then we can make a generating series Φ_{L x T}(x) and compute coefficient [x⁹]
• Product Lemma (1.8.2): Let A and B be sets with weight functions w_A, w_B. Let w be the weight function for the set A x B, defined as w_A(a) + w_B(b) for (a,b) in A x B. Then Φ_{A x B}(x) = Φ_A(x) + Φ_B(x)
• remark: can be generalized to any number k of separate generating series for a k-tuple

Chapter 2

Compositions of a number are basically tuples, whose elements add to to the number (natural numbers), and we say it has k parts for a k-tuple

• a counting problem is how many compositions of n are there with k parts?
  • rewritten/generalized, given a set S and a weight function w: s -> P0,1,2,...} how many elements of S are there of any given weight n?
  • [x^m] Φ_S(x) is the generating series for S with respect to w
  • compositions can be written as caresian products, and thus be described by generating series: k parts is N^k
  • all compositions with 1 part
  • recall we can use the product lemma, and use a weight function for natural numbers

Binary strings

The weight function for the string is the length of the string

• Φ_{A U B}(x) = Φ_A(x) + Φ_B(x); Sum lemma, iff A U is unambiguous

Star Lemma states that if A is a set of binary strings and A * is unambiguous, then the generating series for A * is 1 / (1 - Φ_A(x)) with respect to the weight function equal to the length. Note, the geometric series shape

• proof, start with the sum lemma to break down the fact that A * is A0, A1, A2, A3, A4 ... and their weight functions are the same
• since it is unambiguous, it behaves like a cartesian product and thus we can apply the product lemma
• by applying the product lemma, the sum of the same term raised to the k allows us to apply the geometric series formula
• notice we can only perform substitution because the constant term is 0
  • if B(x) is a FPS with [x⁰]B(x) = 0, then we can substitute. [x⁰] B(x) means no elements of weight 0. empty string not in A means no strings of length 0. since it was unambiguous, the empty string cannot be in A

b is a substring of s if s = abc

Block decomposition is breaking a string into blocks of consecutive 1's or 0's: {1}*({0}{0}*{1}{1}*)*{0}*

• 1-decomposition is breaking a string into blocks with exactly a single 1 (0-decomposition defined similarily)

Chapter 3

We have rational function results, and often want to find [x^n] f(x)/g(x)

• we can use partial fraciton expansion, which works well because we get a sum of terms of the form i/(j-kx), which we can use the geometric series to simplify
  • recall with partial fraction expansion, we use long division to get the factors of the denominators
  • numerator must be less than denominator, so we can divide it out so that we can an integer plus a rational
  • repeated roots, like (x-1)^2 must be written as A/(x-1) + B(x-1)^2

We now use recurrences to get the coefficients (example: fibonacci sequence, where the nth term is described in terms of previous terms like n-1 and n-2)

• we did an example by brute forcing and noticing a pattern
• homogeneous linear recurrence if for n ≥ k, an = q₁a_n-1 ... q_ka_n-k, with given initial coditions from 0 to k-1
  • linear because all a are in separate terms to the first power
  • homogeneous since the total degree of each term is the same
• the characteristic polynomial of this recurrence is C(y) = y^k + q1y^(k-1) + ... + qk

Important takeaway: for a rational function f/g, where deg(f) < deg(g), we can use partial fraction decomposition to break the rational into terms of the form c/(1-ax) or some variant.

• If each denominator is written as 1-ax, then we can simply compute the x^n term of f/g by summing ac for each term

We can also find recurrence relations for An from the generating series by taking the denominator polynomial and converting any x^i term to A_{n-i}, then solving for An.

Chapter 4

Graphs are a set of verticies and edges. Isomorphism is a relation between to graphs that describes two sets the are effectively the same.

We can represent graphs using either the adjacency matrix or the incidence matrix. Adjacency between two vertices occurs when they are joined by an edge. A vertex is incident to edges that join it to another vertex.

The adjacency matrix is defined as a p x p matrix A = [a_ij] where a_ij = 1 if vi and vj are adjacent and 0 otherwise. Notice that this is symmetric since (1,2) and (2,1) would both be marked 1 as a result of an edge.

A walk is an alternating sequence of edges and vertices. A trail has no repeated edges while a path has no repeated vertices.

• a graph is connected iff for all vertices there exists a path between them

Graph colouring and Bipartite graphs

Colouring is useful for register allocation.

• if G is a bipartite graph, then every subgraph of G is also bipartite
  
• every odd cycle is nonbipartite
• G contains an odd cycle iff the graph is nonbipartite

Proof: let C_2k+1 be a cycle. Assume that it is bipartite and Let (A,B) be a bipartition. Adjust notation so that v1 in A and thus v2 in B, v3 in A, ... In fact, vi in A iff i is odd. Now v_2k+1 in A. But v1 and v_2k+1 are edges, and both in A. This is a contradiction.

And there's some intuition that we can use (but not prove yet), that if a graph is not bipartite, then it contains some odd cycle as a subgraph. This is why 2-colourable graphs are very easy to solve, while 3-colorable or more is very difficult (there doesn't exist any proof that let's us take a shortcut).

For n ≥ 1, the n-cube is the graph whose vertices are the binary strings of length n, and two strings are adacent <=> they differ in one bit:

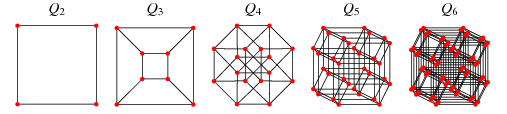
Since each vertex is adjacent to anything differing by 1 bit, then each n bit can differ, so it is incident to n edges. We also have 2^n. Finally, by the handshaking lemma, we have 2^n•n/2 number of edges.

The cut induced by a set of verticies denoted by δ(X) is the set of all edges that have one end in X and the other in X'.

• δ(X) is symmetric to δ(X') and is the set of edges that result from a partition (X, X')
• a graph is not connected iff exists a non-empty subset of X of V(G) s.t. δ(X) = 0

Hamiltonian Cycles go through all verticies of a graph.

Eulerian Circuit is a closed trail which every edge is used.

A 4-regular graph cannot have a bridge

• an edge e is a bridge of G iff G has no cycles containing e

Trees

All edges are bridges. Exactly p vertcies and p-1 edges.

• T is a spanning tree of G <=> T is a maximal subgraph without cycles <=> T is a minimal subgraph that is connected
• BFS can be used to find a spanning tree of a graph
• level of a vertex in T is the # of times we must follow parent to get to the root
• for T a BFS tree of G, every non-tree edge e joins vertices that are at most one level apart

Planarity

planar embedding is a drawing of G on a plane such that no edges cross

• a graph has no planar embedding iff it can be drawn on a sphere
• planar embedding breaks surface into faces
• boundary of a face F is all edges and vertices that are incident with F
• degree of a face is length of the closed boundary walk
• any tree is planar with exactly one face since no cycles
• dual handshaking lemma for a planar embedding of a connected graph G, sum of all degrees of faces is 2 x |E(G)|
• Euler's formula for all planar embedding of a connected graph G, v+f = e+2
• for induction proofs with graphs, remove instead of add
• Euler's Formula can be used to prove that graphs are nonplanar
  • 7.5.3 gives q ≤ 3p - 6, a linear bound for the number of edges in a planar graph
  • 7.5.6 gives q ≤ 2p - 4, another linear bound for triangle free planar graphs
  • only useful for disproving planarity
• subdivision of a graph J is any graph H that can be obtained from J by replacing every edge by a path of length ≥ 1
• kuratowski theorem says that a graph G is nonplanar <=> G has a subdivision of K5 or K3,3 as a subgraph
• K_r r≥1 requires r colors and is in fact r-colorable
• 4 color theroem: every planar graph is 4-colorable.
• 6 color theroem, easier to prove: we do it by induction on p=|V(G)|. The key thing here is that we show there is always a vertex of at most degree 5 (for planar graphs) and the IH is assuming that for some number of vertices less than p, we have a 6-colorable graph

Matching

Some subset of edges such that every vertex is of degree 1 or 0

• a matching is perfect if it contains every vertex