Data Structures and Data Management

• storing, accessing, performing operations on large collections of data

Summary

• for exists proofs, we can keep using the properties of inequalities to simplify the statement

Introduction

Problem

Given a problem instance I (input) find a solution (output with correct answer) in finite time with Size(I)

Example:

• Problem: multiply two matricies
• Instance: Two matrix inputs
• Solution: One output matrix

Running Time Simplifications

Matrix multiplcation performs in n²(n+n-1) time or O(n³) in naive implementation

• Strassen's Algorithm n^log2(7)
• Le Gall n^2.37

Order notation:

• f(n) in O(g(n)) if exists constants c > 0 and n₀ > 0 s.t. 0 ≤ f(n) ≤ c g(n) forall n ≥ n₀
• O describes the set of functions asymptotically upper bounded by function g
• Ω describes the set of functions asymptotically lower bounded by a function g
• Θ describes the set of functions asymptotically equal to g
• o is describes functions strictly less than g
• ω is strictly greater than g
• c offsets a transformation of the function, while n0 describes the "sufficiently large" factor during comparison

"Best Case & Worst Case" refer to instances of inputs into the algorithm, but this has nothing to do with upper/lower bounds. Lets look at a contrived example:

• best and worst cases can have a range; suppose we introduce a probabilistic, nondeterministic factor (contrieved example in class)

Proof: first derive an appropriate c and n₀, then show that desired relationship holds for all n ≥ n₀

• 0≤2n2+3n+11≤cn2 foralln≥n0.
• exists some c > 0, and n0 > 0 s.t. 2n² + 3n + 11 ≤ cn²
• n² ≥ n forall n ≥ 1

Prove that 2010n2 + 1388n ∈ o(n3) from first principles.

• if 2010n² + 1388n in O(n³), then forall constants c > 0, exists n0 > 0 s.t. 2010n² + 1388n < cn³ forall n ≥ n0
• now we can simplify the expression by subbing n squared for n
• 2010n² + 1388n² < cn³
• 3398n² < cn³ for n ≥ 1
• 3398 < cn, n ≥ 1
• n0 > 3398/c, c > 0
• n0 = 3398/c + 1, since n ≥ 1
• now prove for n ≥ n0
• 3398 < cn
• let n = n0 + k, k ≥ 0
• 3398 < c(3398/c + 1) +ck
• 3398 < 3398 + c + ck
• 0 < 1+k, since k ≥ 0, we can set k = 0
• 0 < 1, therefore true

Now let's compare two implementations of exponentiation:

Bruteforce(b,x) we iteratively call ret *= b x times
Squaring(b,x) we recursively call ExpSquaring(b*b, x/2) or b*ExpSquaring(b*b, (x-1)/2)

we see that Tb(x) = x, and Te(x) = {3log2(x), 4log2(x)

Loop Analysis

Start from inner-most loop, and use Θ-bounds throughout to obtain a θ-bound for the complexity of the algorithm

• identify elementary operations of θ(1)
• complexity of loop is expressed as the sum of complexities at each iteration
• use maximum rules whenever to simplify: that is O(f(n) + g(n)) = O(max{f(n), g(n)})

Priority Queue

Priority Queue is an ADT with a collection of items (associated with a priority)

• insert: with tagged priority
• deleteMax: remove the item with highest priority

Heaps are a type of binary tree. A max-heap has additional properties:

• heaps are balanced & left justified
• heap-order proerty says that any node's children have equal or lower priority
• since the height of a heap is Θ(log n), then insertion and deletion operations are also O(log n)
• our insert will simply add the element in the last slot, then "bubble up"
• our delete will shift the last element into the first slot, then perform swaps again by "bubble down"

Sorting and Randomization

• kth element in the array in not easy; we need to manipulate to get it
• for a given element, it is easy to find it's index if the array was sorted in O(n)
• quick select uses this intuition; pick a pivot, and restructure the array by partitioning, then the pivot is in it's correct place
  • assuming all n! permutations are equally likely, average cost is the sum of costs for all permutations, divided by n!
  • T(n,k) is the average cost for selecting the kth item from size n
  • general case: i is the index of our pivot in a sorted array, (n-1)! are the total number of possible positions once we've selected our i. throwing away i+1 elements after partitioning
  • below, we've described below as
    

Randomized algorithms

• relies on some random numbers, from a PRNG, a deterministic program that uses a true random seed
  • the goal is to have a uniform distribution over our desired range, while making the period of repetition large enough that it is negligable
• basic example: Von Neumann 1946 "Middle squared method", takes a seed of 4 digits, squares it, pad/truncate to get an 8 digit, then return
• the motivation is that we don't have control over input (bad instances), but we can control the random numbers, to shift the probability distribution from what we can't control

Average vs expected running time

• the Expected running time of a randomized algorithm for a particular input I is the "expected" value of T(I,R)
  • for T, calculate the sum of T(I,R) • Pr[R] (think weighted average) and assuming uniform distribution of R, we get simply the mean runtime across all R
• the motivation behind randomized quickselect is that we have a very small chance of sorting an array by shuffling (2/n!)
  • first idea: sorted arrays are worst case for quickselect since we select element 1 and never have a left partition, so O(n^2)
  • second idea: randomize the pivot, by choosing a random pivot
• Worst-case linear time partitioning called "medians-of-five" for pivot select. Partition into groups of five, find each median and take the median of medians, then we can say in Θ(n) run time the number that is highly probable to be close to the actual median
  • mutually recursive, and can be shown to be θ(n) notice they call each other recursively

Sorting

Comparison sorts are lower bounded at Ω(n log n)

• decision trees
• HeapSort is the only fast algorithm with O(1) space
• QuickSort is often the fastest
• CountSort and RadixSort can achieve o(n log n)

Radix Sort

• R is the base, m is the number of digits, then we can represent x = x0 R^0 + ... + x_m-1R^n-1
• MSD (most significat digit), bucket based on digit and apply a sorting algorithm to sort each bucket
• LSD (least), bucket again based on the least significant digit, and use a stable sort, otherwise lose previous work done on lesser digits
  • can be written iteratively,
  • runningtime of LSD: Θ(m(n+R))
  • space used Θ(n+R): array B for n and array I and C for indicies and counts

Quick Sort vs Merge Sort, quick sort has a slower worst-case, but under expected case, they are comparable. But quick sort retains order and is an in place sorting algorithm

Tail call elimination can be done using loops to reduce the number of stack frames, and optimized further by only recurising on the smaller partition

Tutorial: if A is a partial sorted array where n^k elements are already sorted, 0 < k < 1, then we can sort the remaining elements in Θ(n) time. First use merge-sort in Θ(n^k log (n^k)) = Θ(kn^k log n) = Θ(n^k logn) in o(n) since log n is smaller than n^c for any c > 0 and since k < 1.

Consider Stooge Sort: partition sort by thirds. The sort A1 U A2, sort A2 U A3, then finally resort A1 U A2. By the algorithm, we know the recurrence is

T(n) =

• Θ(1) if n=1 or n=2
• 3T(2n/3) + Θ(1) if n ≥ 3
  • three sub problems, of size 2n/3
• simplifies to 3^k T((2/3)^kn) + d•3^i, i from 0 to k-1
• we need log base (2/3)^k n = 1, 3/2 n = K recurences to reach the base case
• 3^k T(1) + d(3^k - 1/2)
• Θ(3^k) or ~ O(n^2.71)

Consider Bogo sort. We want the expected case running time. To do so, take a probabilistic approach: T(n) = 1cn + (1/n!)d + (1-1/n!)T(n). Note that this is a probabilistic analysis, so each coefficient is just a probability. 1cn is 100% chance to shuffle n object and check n objects if they're sorted.

• T(n) = cn + (1/n!)d + (1 - 1/n!)T(n)
• T(n) = n!(cn) + d
• T(n) in Θ(n•n!)

Dictionary ADT

Tries

Tries, or Radix Tree, are a dictionary for strings. The basic trie is for binary strings and is thus a binary string.

Compressed Tries (Patricia Tries) store extra information at each node. They store which bit position the next strings differ at, allowing us to encode strings with idential portions very efficiently.

Skip List

Inserting into a skip-list, we can use RNG to determine the height, based on a binary string seed.

• each height has 1/2^h probability of occurring
• SkipSearch(L, x) returns an element before the element x

We can make modifications to a linked list to optimize search times

• transpose huristic swaps searched element 1 closer to the front
• move to front moves searched elements directly to the front

Midterm

• first principles runtimes
• AVL Insert O(log n), Delete O(log n)
  • know rotations
• Dictionary tricks for linked lists (move to front and transpose)
• Heap Insert O(log n), Delete-Max O(log n), Heapify O(n)
• Heapsort, Mergesort, Quicksort
• quickselect expected O(n), count sort O(n + R), radix sort O(m(n+R))

Multi-dimensional Data

d-dimensional data, with aspects/coordinates

• operations insert, delete, rage-search query
• for range searches, we could either use a sorted tree or a binary search tree; O(log n + k), k is number of inside nodes
• d-dimensional dictionaries can be squashed to a single dimension, but range searches on single aspects are lost
• partition trees has n leaves, one for each item, and each internal node corresponds to a region
• Quadtrees are partition trees, where each node corresponds to a square in the cartesian plane, the root of which contains all
  • each node has 4 children, the 4 subquadrants of the given square
  • points on split lines belong to left and bottom
  • can be used for compression, image processing
• kd-trees aim to optimize what quadtrees do, by splitting each region in half by the median using alternating vertical and horizontal lines using the median to split equally
  • usually pretty balanced, so building takes O(n log n)
  • by convention when building the binary tree, above in grid is left, below is right
  • range search operation: O(# nodes on boundary + output)
• range trees are trees of trees for points, built by sorting x and with each node having an associated tree sorted on y
  • associated tree holds the same subtree as the node sorted on x, but it instead is sorted by y
  • insert: log n for x coordinate lookup, then for each log n parent, insert into each associated tree in log n time for y

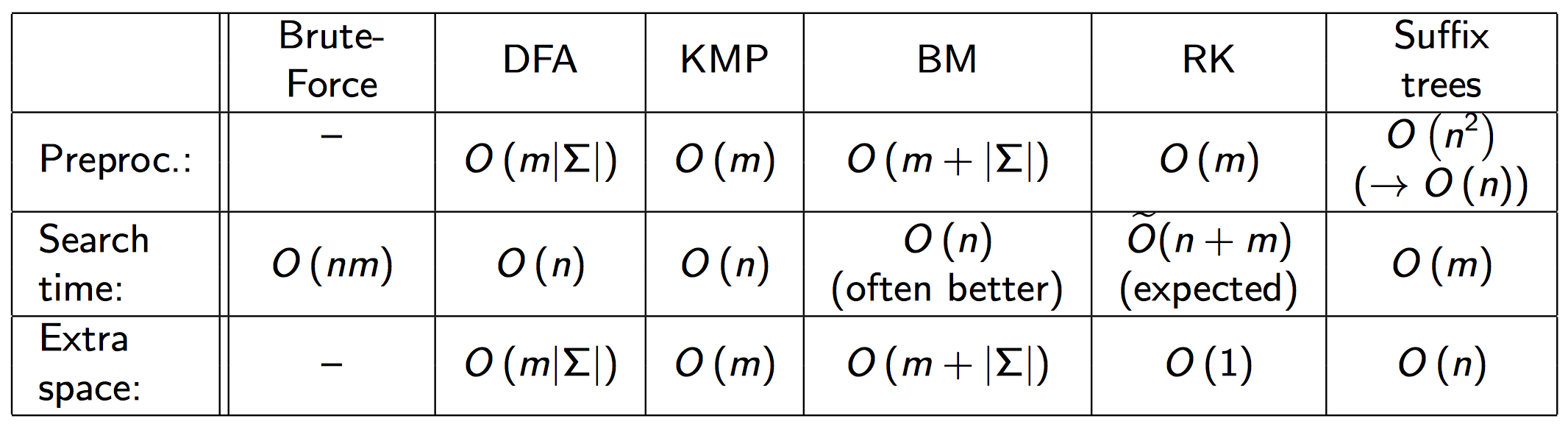
Pattern Matching

DFAs give us a nice representation of how we can reuse information about the state of what we've matched thus far. Refer to cs241 notes for details.

KMP matches left to right, and shifts the pattern upon a bad match based on the largest prefix of our pattern that is a suffix of what we've matched so far.

• build a failure array during preprocessing, which acts as an easy lookup for what the most efficient shift would be (and this simply implements DFAs in practice)
• runtime is Θ(m) to build failure array and Θ(n) to run KMP, where m is the length of the pattern and n is the string length
  • note there is no more than 2n iterations of either algorithm because the worst case is that each element is iterated by both the right and left iterators as we walk along string T

Boyer-Moore is reverse order searching (right to left)

• we move the pattern left to right as usual, but when checking the pattern, we'll go right to left
• the goal is to shift the pattern as much as possible when mismatches occur
• bad character jumps skip the entire pattern length if it finds a character in string T not in P
• good suffix jump let's us shift P right to align with the next leftmost occurence of the suffix (not including the bad match character)
• Good suffix array is what we build during preprocessing of the pattern

We have to build two extra data structures to perform BM: Last occurence function and good suffix array

• for good suffix array, at each i of the array, where i represents the m-i length suffix, we want to find the rightmost occurrence (the next occurrence) of the suffix that we've correctly matched so far
• recall in BM, we're iterating from right to left when checking the pattern, so it makes sense we want the rightmost occurence of the right suffix
• for the implementation, we choose element at i to represent the next index of the pattern that shares the same suffix, excluding P[i], the ith character of our pattern, because when we mismatch, we can reuse the matched suffix and shift the pattern to check the next portion of the pattern that's different but share some suffix

Rabin-Karp Fingerprint uses hashing to compare our pattern to a substring (think hashing to check if your downloaded file is correct)

• after hash values are equal, do a full string comparison to guarantee correctness
• run time is Θ(mn), since it's possible that each n characters causes a hash collision, follwed by m iterations through the length of the pattern to verify that it is not a correct match
• in practice, our runtime is O(m + n), iterate through our match to check correctness and iterate through n characters to find substring

What if we want to search many patterns on the same text? Then preprocess text T

• use a trie that stores all suffixes of text T called a suffix trie
  • side note, not all substring, but instead only suffixes, so the last letter of our text is in every suffix

Compression

Transmission and storage of data

• source text S, coded text C, each with their own alphabet ∑
• judge encoding schemes by speed, reliability (error correcting), security/encryption, size
• compression ratio |C| log ∑_C / |S| log |∑_S|
• logical compression only applies to certain domains
• ASCII is a character encoding
• prefix-free is when no string in an alphabet is a prefix of another
  • important since we can do decoding with a dictionary resulting in a sort of "short circuiting"
• Huffman coding, each character of ∑ is a leaf of the trie
  • uses static dictionary which doesn't change for the entire encoding decoding
• run-length encoding is a variable-length code with fixed decoding dictionary (not explicitly stored)
  • blocks of 0s and 1s are runs
• prefix-free integer encoding has some leading number of 0s followed by the binary representation of a number
  • this scheme is prefix free since we have uniquely defined each number by adding leading 0s
  • number of 0s is the length of k in binary - 1
• Adaptive Dictionaries in contrast to static, starts out with a usually fixed dictionary (set of characters like UTF) but after writing the ith character to output, both encoder and decoder update D_i to D_i+1
  • Huffman and RLE make use of physical characteristics like repeated single characters
  • in certain domains of text, there are very common substrings (think html tags)
• Lempl-Ziv is a family of adaptive compression algorithms
  • each character in the code corresponds to exactly a character or substring
  • GIF uses LZW
• LZW is fixed width encoding using k bits
  • store decoding dictionary with 2^k entries (the number of possible permutations)
  • first |∑s| entries are for each single character
  • encoding algorithm: walk through text S, populating the remainder of dictionary by gradually adding new substrings based on the longest token that we've seen so far, appended with the first mismatch, creating a new substring in our dictionary
  • decoding: same idea, build dictionary while reading strings and this seems to work well since both sides are deterministic, and doesn't involve explicitly storing the dictionary with the text
    • in the case that the decoder is one step behind encoder, s = s_prev + s_prev[0]

Text Transformation

Preprocessing our text so that we can make better use of compression algorithms

• move to front huristic

Burrows-Wheeler Transform is a compression technique, that reorders the characters in the text, to be more easily compressible with Move To Front

• is a block compression method
• BWT, followed by MTF, RLE and Huffman is the algorithm for bzip2
• a cyclic shift is shifting all characters some i distance, and wrapping back to the start past index n

Encoding for BWT:

1. place all cyclic shifts (or rotations) of S in a list L (n^2 size list)
2. Sort the strings in L lexicographically (alphabetically, $ is last)
3. Make a list C, of last characters of each string in L

Decoding for BWT, given string C from encoding:

1. make an array A of tuples (C[i],i)
2. Sort A by the characters ($ is first, same characters are sorted by their i increasing) into array N
3. set j to index of $ in C
4. recursively set j to N[j] (kind of a linked list structure) and build output string S appending C[j] to S

The reason this works well is because sorting all possible rotations will group any repeated substrings together in the encoding phase, for list L. It happens that the last character of each rotation will correspond to the first character of exactly another rotation, and since we've sorted it, all occurences of some substring in the text gets grouped together. This happens not only for the first letter of the substring, but also each subportion of repeated characters will have its characters grouped together.

It's pretty remarkable that the output is simple and deterministically reversable through decoding. We can think of the inverse as, at any iteration of our decoding, we can treat the last column as the letter that preceeds some prefix of a rotation. Since we have all possible rotations, at every step of the recursion, we can always place each letter of C at the start of the corresponding string and resort. This gives us a new list of reordered, possible prefixes that must all exist because of the property of rotations. Our decoding algorithm is just a restricted set of instructions to perform this.

Memory

2-3 Trees are better than AVL trees since loading pages is expensive, and AVL trees do the Θ(log n) page loads

• binary search tree structure, but with the possibility of two keys and three children at an internal node
• leaves don't store keys, and are assigned NIL
• insertion follows a sort of bubble up process
  • find the lowest internal node where the new key can be added to, then if we have three keys, push the middle up, recursively
• structurally, for each node, we have k keys and k+1 children (so 2 keys, 3 children or 1 key, 2 children, so that we can do lookups at the k+1 positions between the keys), and all leaves need to be at the bottom layer (so the trees always balanced)
• deletion has a bunch of cases, but generally we first swap the KVP with its successor recursively, until the key is a leaf (before the NIL layer)
  • case 1, the leaf is a 2-node, in which case we simply delete the key which leaves behind a 1-node
     - case 2, if 1-node, we leave an empty node which is unbalanced, so we want to rotate (or "transfer") such that the result is still balanced while preserving structure. Deletion of a child of a 2-node means we do a sort of partial rotation. But transfer only works for immediate siblings (adjacent). If not sibling, we merge down from the parent.
  • case 3, 1-node deletes one of its children, then merge the whole subtree into a 2-node. Then the parent is an empty node, so merge one parent down. This may result in recursive merge calls down.

B-Trees is a generalization of 2-3 trees. An (a,b)-tree of order M:

• each internal node has at least a children (except the root which can have at least two children), and at most b children
• same structural properties, for k keys, k+1 children
• B-tree of order M is a (ceil(M/2),M)-tree
• lower bound for height of a B-tree is Θ((log n)/(log M)), analyzing number of nodes and number of KVP per node
• in external memory, we want to use a B-tree of order M, s.t. an M-node fits in a page (with 32 byte values, M = 10.5 ~= 10)
  • in this case, we only load Θ(logn/logM) instead of Θ(logn) as is the case in AVL trees

Hashing in external memory may result in lots of disk transfers since data is often scattered. This gets worse when we use things like cuckoo hashing

• with linear probing, cache misses result in hash table accesses being in the same page
• exendible hashing is similar to B-trees with height 1 and max size S at the leaves
• the directory stored in memory is based on the first α digits, which hashes to 2^L possible keys and we store the first d digits of the hash key for the directory
  • key prefixes in directory point to blocks of S items (think pages in external memory)
• blocks are shared, so that every block stores a local depth kB ≤ d, which says how many digits are shared amongst all keys in the block
  • hash values agree on leading kB bits
  • 2^(d-kB) directory entries point to the given block B
• so again, we specify S, the max size of each block, and d, the size of key prefixes in our directory, then the directory entries point us to blocks. When the number of keys in a block exceeds S, the block needs to be split
• insertion, put in corresponding block unless block is full, starting with one block. Then we split B into two blocks when the keys in the block B exceed S. Separate according to kB+1, and split on 0 vs 1
  • if the block is full and kB = d, perform a directory grow, where we double the directory size (d += 1)