Linear Algebra Review

• Matrix multiplcation AB = C, is every column of A, dotted with every row of B
• Identity Matrix is related to the inverse Matrix: if Ax = b then Ix = A^-1b, so A is invertible iff exists

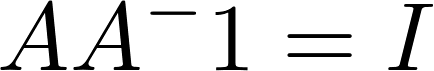
• A is invertible iff it has exactly one solution for every value of b
• span of a set of vectors is the set of all points obtainable by linear combinations of the original vectors
• linear dependence occurs when a vector in a set can be described as a linear combination of other vectors in the set
• norms are used to measure the size of vectors; norms are functions that:
  • f(x) = 0 => x = 0
  • f(x + y) ≤ f(x) + f(y)
  • forall a . f(ax) = |a|f(x)
• L^p norm = (∑|xi|^p)^1/p
  • notice that for p = 2, we get euclidean distance. So L² is the euclidean norm
• L¹ norm is better for machine learning, since it grows linearly near the origin (good to discriminate between c exactly zero and close to)
• Symmetric Matrices: A = A^T
• Orthogonal Matrices: AA^T = I
• a linear transformation
  • is analogous to a linear function in one dimension
  • representable by a vector field
• decomposition is useful in math, like prime factorization
• eigendecomposition is breaking a matrix into eigenvectors and eigenvalues
  • eigenvector is defined by Av = λv, so the vector's direction is unchanged through matrix multiplication
  • eigenvectors can be rescaled to any vector sv for s ≠ 0, so we look for unit eigenvectors
• let V be the concatenation of eigenvectors for A as columns. Then A = Vdiag(&lambda)V^-1
• determinant of a matrix can be thought of as the expansive multiplicative factor
  • equal to the product of all the eigenvalues
• a basis of a vector space is a set of vectors that are linearly independent, and can express any vector in the vector space as a linear combination of the basis vectors. We can represent a set of vectors as a matrix
  • a basis is linearly independent spanning set of the vector space
  • for set of vectors S, the span W is the intersection of all subspaces containing S. then S is a spanning set of W
• eigenspace for an eigenvalue λ E_λ is the set of all vectors (eigenvectors) that satisfy 0⃗ = (I•λ - A)•v⃗
• dense vectors can be used to optimize storage, reducing storage for sparse vectors that are mostly 0s
  • [0,0,0,0,1,0,0,0,3] => [(4,1), (8,3)]

Probability & Information Theory

• Marginal Probability is the distribution over a subset of variables (denominator is the summation of individual probabilities in the subset)
  • different than conditional probability in that it is not contingent on a value of a variable
  • for continuous probabilities, we use an integral
• Chain Rule: P(a,b,c) = P(A|b,c)P(b,c) = P(A|b,c)P(b|c)P(c)
• x,y are conditionally independent if conditional probabilities given z P(x,y|z) = P(x|z)P(y|z)
• Bernoulli Distribution φ ∈ [0,1], the probability a variable is equal to 1
• important sometimes to have a sharp point at x = 0, with exponential distribution or adjusted to some point μ using laplace distribution
• Structured Probabilistic Model plots multiple variables on the same graph
  • factorization of distribution into smaller distributions, dependent on less variables
• KL Divergence or information difference is asymmetric difference between two distributions P and Q; q * = argmin_qD_KL(q||p)
  • KL Divergence from P to Q, D_KL(P||Q) is the amount of information lost when Q is used to approximate P
• can draw an undirected graph over random variables, showing how the probability distributions can be factored

Information Theory revolves around quantifying how much information is in a signal

Logistic Regression

Regression model where the dependent variable is categorical

• includes binary dependent variables
• multinomial logistic regression if more than two categories
• ordinal logistical regression
• logistic functions take real input and output a result between 0 and 1 (interpreted as probability)
• standard logistic function S(t) = σ(t) = 1/(1 + e^-t) ∈ (0,1), a type of sigmoid function

Numeric Computation

Overflow and Underflow are two problems when represented infinitely many real numbers with finite bit strings

• exponential expressions can easily overflow or underflow
• softmax = exp(xi)/∑(exp(xj), which can evaluate to 0 very easily with small numerators, and log softmax to -infinity
• stablization is important to avoid these rounding errors

Conditioning refers to how quickly a function changes with respect to small changes to input

• poor conditioning occurs when a function's output can be greatly effected by input rounding errors

Most learning algorithms involve optimization, specifically minimization of functions

• notationally, * denotes minimization, so x^* = arg min f(x)
• minimization occurs on functions of single output (may be a vector function)
• gradiant of f at point x (for vector x), the vector containing all partial derivatives: ∇_xf(x)
• critical points in multi-dimensions are where all partial derivatives are 0 in the gradient
• directional derivative with respect to a is f(x + au)
• gradiant descent is the process of finding the directional derivative at each step that minimizes the vector function the most
• min ||u|| ||∇f(x)|| cosθ
• gradient descent proposes a new point x' = x - ∈∇f(x), ∈ is the learning rate
• evaluated iteratively evaluating f(x - - ∈∇f(x)), and ∈ can be determined by trying multiple &sin; values and picking the smallest result (line search)
• gradients are a generalization of the concept of derivatives, for vector functions
• Jacobian is a generalization of the gradient, for vector-valued functions

Jacobian Matrix J corresponds to a function. It contains all partial derivatives of a vector field: J_i,j = ∂/∂xj • f(x)_i, where f(x)_i denotes the ith output as a function of the vector x (we can think of a vector field as a vector of vector functions)

• second derivatives are important to determine curvature of the function
  • can be used to determine dead ends (linear functions) or divergence
• Hessian Matrix is the Jacobian of the gradient (gradient is a vector of vector functions, a vector field for a given point)
• forall points where all partial derivatives are continuous, the differential operation is commutative, so H_i,j = H_j,i and therefore the Hessian matrix is symmetric (true for nearly all points in most fields)
• since the Hessian Matrix is real and symmetric, it can be decomposed into an orthogonal basis of eigenvectors
• second derivative in a direction d⃗, d⃗ is a unit vector, we use the Hessian matrix, and its eigenvectors, with the result being some weighted average of all eigenvalues (depending on its proximity to each corresponding eigenvector), and since the eigenvalues describe orthogonal eigenspaces, we can weight from 0 to 1 for each eigenvalue based on the angle between d⃗ and their corresponding eigenvectors
  • if d⃗ is an eigenvector, than the second derivative is its eigenvalues
  • the second derivative is bounded by the largest and smallest eigenvalues
• the directional second derivative tells us how well we can expect a gradient descent step to perform
• we approximate f with the second order taylor polynomial: f(x) = f(x0) + (x - x0)^T∇_x0f(x) + 1/2(x - x0)^TH_x0(x - x0)
• second derivative tells us whether it's a saddle point, or local max/min
• Newton's method can improve time, in that it can converge in less iterations that gradient descent
  • based on second order taylor series expansion to approximate f(x), then repeatedly jumping to the approximation's minimum
• gradient descent is a first-order optimization while Newton's method using the Hessian is a second-order optimization algorithm
• Newton's method can converge on a saddle point very easily, as the first and second directional derivatives are 0
• Convex optimization provides more guarantees than regular optimization, by only working with convex functions, strongly restricted
  • convex functions have positive Hessians everywhere, since there are no saddle points and any local mins are global mins
• Lipschitz continuous functions have their rate of change bounded by a Lipschitz constant L: forall x, y . |f(x)-f(y)| ≤ L |x-y|
  • useful for bounding gradient descent's learning rate, for better accuracy
• Constrained Optimization operates on a subset of a function domain
  • often simply modify gradient descent, taking constraint into account
  • apply gradient descent, then project the value into the set of feasible points S
  • more sophisticated, phrase the problem as an unconstrained one
• KKT provides a general solution for constrained optimization, by introducing a new function called generalized Lagrangian
  • describe the constrained set S in terms of n equalities, g⁽ⁱ⁾(x)=0, and inequalities h^(j)(x)≤0
  • introduce variable coefficients λ_i and a_j corresponding to each constraint